Průměr, medián a modus představují míry polohy (lze je nazvat i mírami centrální tendence). Tyto míry nám říkají, kolem jakého čísla se hodnoty nacházejí, neboli, kde je “střed” hodnot. Možná vás napadá otázka, proč jich potřebujeme tolik? Protože každá z nich tento „střed“ popisuje trochu jiným způsobem. Pojďme se na ně blíže podívat:
- Aritmetický průměr je součet všech hodnot v souboru dělený jejich počtem.
- Medián je prostřední hodnota (seřazených hodnot) v souboru.
- Modus je nejčetnější hodnota v souboru.
Z těchto tří charakteristik je aritmetický průměr jediný, ke kterému potřebujeme vzorec. Medián a modus obvykle zvládneme i bez vzorce ?
Aritmetický průměr
Většinou když někdo řekne průměr, myslí tím klasický aritmetický průměr. My se časem dozvíme, že existují i jiné typy průměrů, ale to si řekneme až někdy příště. Aritmetický průměr se používá pouze u číselných proměnných a nejčastěji ho najdeme ve dvou formách, v prostém a váženém tvaru. Pomocí prostého i váženého tvaru dojdeme při správném použití ke stejnému výsledku. Vážený tvar nám většinou šetří čas a to je v dnešní době velmi důležité.
Pojďme si to ukázat na jednoduchém příkladu:
Máme soubor hodnot: 5, 10, 10, 20, 20, 20, 50 a naším úkolem je spočítat průměrnou hodnotu.
Výpočet pomocí prostého aritmetického průměru:
\overline{x}=\frac{\sum{x_{i}}}n=\frac{5+5+10+10+20+20+20+50}{8}=\frac{140}{8}=17,5
Výpočet pomocí váženého aritmetického průměru:
\overline{x}=\frac{\sum{x_{i}n_{i}}}{\sum{n_{i}}}=\frac{5*2+10*2+20*3+50}{2+2+3+1}=\frac{140}{8}=17,5
Nemělo by vás překvapit, že výsledky jsou stejné! Rozdíl je pouze v tom, že vážená forma dokáže zohlednit četnost/váhu jednotlivých hodnot a velmi často usnadní výpočet. Doporučuji ho tedy v případě, kdy hodnoty mají přiřazené váhy a nebo je v souboru více stejných hodnot.
Medián
K výpočtu mediánu není potřeba žádný složitý vzorec. Medián nalezneme tak, že hodnoty v souboru seřadíme (od nejnižší po nejvyšší hodnotu) a najdeme střed. Nalezení prostřední hodnoty se liší v závislosti na tom, zda máme lichý nebo sudý počet hodnot. Pokud pracujete se sudým počtem hodnot, tak medián je průměrem dvou prostředních hodnot. V případě lichého počtu je prostřední hodnota jen jedna.
Pojďme si to opět ukázat na našem příkladu:
5,5,10,\underline{10},\underline{20},20,20,50
Můžeme vidět, že prostřední hodnoty jsou 10 a 20 a medián \widetilde{x} je tedy 15 (\frac{10+20}{2}=15).
Medián se používá převážně u číselných (kvantitativních) proměnných, ale lze ho určit i u proměnných ordinálních. Ordinální proměnné jsou proměnné, které lze seřadit (např. dosažený stupeň vzdělání – ZŠ, SŠ, VŠ). Představme si, že máme následující soubor hodnot: ZŠ, ZŠ, SŠ, SŠ, SŠ, VŠ, VŠ. Máme sedm hodnot a lze vidět, že prostřední hodnota je čtvrtá hodnota a tedy medián je SŠ vzdělání.
Modus
Modus je nejčetnější (nejčastěji se vyskytující) hodnota v souboru. Stačí se tedy podívat na soubor hodnot a určit, která hodnota se zde vyskytuje nejčastěji. Jenže, co když je takových hodnot více, a nebo se v souboru žádná hodnota nevyskytuje vícekrát? I pro takové případy má statistika řešení.
- V souboru není žádná hodnota vícekrát = zpravidla se udává, že modus není, nicméně v některých literaturách lze najít i definici, že mody jsou všechny hodnoty.
- V souboru je jedna nejčetnější hodnota = unimodální rozdělení.
- V souboru jsou dvě nejčetnější hodnoty = bimodální rozdělení.
- V souboru jsou tři nejčetnější hodnoty = trimodální rozdělení.
- V souboru jsou čtyři nebo více nejčetnějších hodnot = multimodální rozdělení.
Pojďme se opět podívat na náš příklad.
5,5,10,10,20,20,20,50
V souboru hodnot lze vidět, že hodnota 20 je zde třikrát a tedy představuje mód. Jedná se o unimodální rozdělení a modus \widehat{x} = 20. V případě, že by zde i hodnota 10 byla třikrát, tak by byl \widehat{x}=10 \ a \ 20.
Modus se hodí primárně pro práci s kategoriálními proměnnými, ale lze ho samozřejmě určit i u číselných proměnných. Dá nám informaci, která z hodnot se v souboru nachází nejčastěji a oproti průměru a mediánu je to jediná míra polohy, kterou lze použít i u nominálních dat.
Která míra polohy je nejlepší?
Výběr vhodné míry polohy závisí na typu proměnné a na tvaru rozdělení. Není tedy jedna správná volba. V případě, že hodnoty v souboru mají normální rozdělení, tak platí, že průměr, medián a modus jsou si rovny. Tuto skutečnost lze vidět na následujícím grafu:


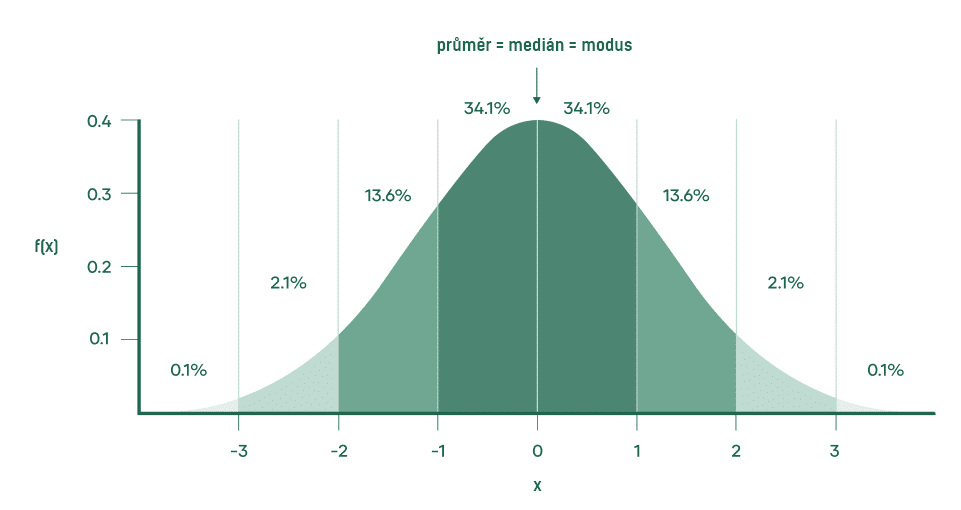
[…] podobně jako míry polohy, je možné měřit několika způsoby. Nejpoužívanějšími charakteristikami variability jsou […]
[…] si zakoupíte 40 koblih a zvážíte je. Průměrná váha vám vyjde 62,6 gramů a směrodatná odchylka 6,99 gramů. Hladinu významnosti zvolíte […]