Chí-kvadrát test nezávislosti je statistická metoda používaná k analýze vztahů mezi dvěma kategoriálními proměnnými. Chí-kvadrát test nezávislosti je základní nástroj statistické inference, který umožňuje posoudit, zda mezi proměnnými existuje statisticky významná závislost. Dá vám odpověď na otázku, zda závisí hodnoty jedné kategoriální proměnné na hodnotách jiné kategoriální proměnné. V tomto článku si ukážeme principy Chí-kvadrát testu nezávislosti, jeho podmínky, aplikaci a interpretaci výsledků v praxi. Jedná se o často užívaný test při vyhodnocování dotazníkových dat.
Princip Chí-kvadrát testu nezávislosti
Jak již bylo zmíněno v úvodu, jedná se o metodu, která slouží k analýze vztahu mezi dvěma kategorickými proměnnými. Jako každý test statistických hypotéz má i chí-kvadrát test nezávislosti jak nulovou hypotézu, tak hypotézu alternativní.
Nulová hypotéza: Mezi kategorickými proměnnými není významný vztah.
(Pokud znáte hodnotu jedné proměnné, nepomůže vám to předpovědět hodnotu jiné proměnné.)
Alternativní hypotéza: Mezi kategorickými proměnnými existuje významný vztah.
(Znalost hodnot jedné proměnné vám pomůže předpovědět hodnoty jiné proměnné.)
Princip Chí-kvadrát testu nezávislosti staví na porovnání pozorovaných (empirických) a očekávaných (teoretických) četností v kontingenční tabulce. V kontextu chí-kvadrát testu je slovo „očekávané“ ekvivalentní tomu, co byste očekávali, pokud platí nulová hypotéza. Jestliže jsou vaše pozorované četnosti dostatečně odlišné od očekávaných, nulovou hypotézu byste zamítali a došli k závěru, že spolu proměnné souvisí.
Jak očekávané četnosti zjistím?
Nejprve se vytvoří kontingenční tabulka, která zobrazuje vztah mezi dvěma kategoriálními proměnnými. V kontingenční tabulce je uveden počet výskytů (četností) v jednotlivých kombinacích kategorií a dále suma řádků a sloupců. Viz. Obrázek č.1.
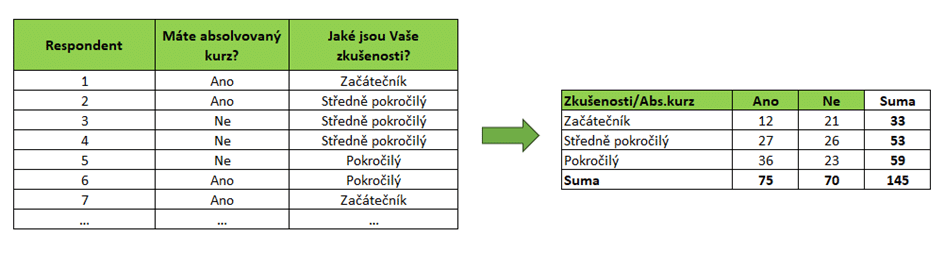
Očekávané četnosti můžete vypočítat na základě dat v kontingenční tabulce. Očekávané četnosti se pro každou napozorovanou četnost vypočítají jako součin sum v daném sloupci a daném řádku, který se vydělí celkovým součtem četností v kontingenční tabulce. Chí-kvadrát test nezávislosti detailně řešením v tomto online kurzu. Zde je dobré zmínit, že většina statistických softwarů je schopna vám očekávané četnosti, včetně kompletního Chí-kvadrát testu, vypočítat automaticky.
Výsledkem Chí-kvadrát testu bude vypočtené testové kritérium, nejčastěji značeno jako „G“ a p-hodnota. Případně je možné k vyhodnocení porovnat testové kritérium s kritickou hodnotou, kterou naleznete ve statistických tabulkách.
Jak výsledky interpretovat?
Pokud je výsledná p-hodnota menší než vámi stanovená hladina významnosti (obvykle 5 %), docházíte k závěru, že vaše napozorované četnosti se od očekávaných četností na dané hladině významnosti liší. Mezi kategorickými proměnnými existujte statisticky významná závislost.
Pokud je p-hodnota vyšší než hladina významnosti, tak nulovou hypotézu nelze zamítnout. Neprokázali jste, že se napozorované četnosti od očekávaných četností na dané hladině významnosti liší. Odpovědí je, že se nepodařilo prokázat, že by mezi kategorickými proměnnými byla statisticky významná závislost. Pro úplnost analýzy doporučuji výsledek doplnit o vhodnou míru věcné významnosti.
Při interpretaci výsledků buďte opatrní. To, že se vám nepodařilo prokázat závislost neznamená, že jste prokázali nezávislost.
Hodnoty v kontingenční tabulce doporučuji komentovat v procentech, nikoli v absolutním vyjádření. Tedy například spočítat kolik procent respondentů má v každé kategorii zkušeností absolvovaný kurz (viz. graf č.1).
Má použití Chí-kvadrát testu nezávislosti nějaké podmínky?
Ano a tyto podmínky byste měli ověřit ještě před samotným výpočtem. Jejich nedodržení může vést k získání mylných závěrů.
-
- Jednotlivá pozorování v kontingenční tabulce jsou nezávislá, tedy každý prvek výběrového souboru je zahrnut pouze v jedné buňce kontingenční tabulky.
-
- Alespoň 80 % buněk kontingenční tabulky má očekávanou četnost větší než 5 a všechny buňky tabulky (tedy 100 % buněk) mají očekávanou četnost větší než 1.
První podmínka by měla být splněna vždy, pokud tomu tak není, nemá smysl ve výpočtu Chí-kvadrát testu dále pokračovat. U druhé podmínky se s nesplněním můžete setkat poměrně často, a to tehdy, když máte málo dat a tím pádem i nízké očekávané četnosti. Řešením může být sloučení některých kategorií, např. „velmi spokojen“ a „spíše spokojen“ sloučit do kategorie „spokojen“, nebo při nízkých hodnotách u více očekávaných četností vytvořit kategorii „jiné“. Důležité je, aby toto sloučení dávalo logicky smysl. V případě, že máte tabulku 2×2 a i tak jsou vaše očekávané četnosti příliš nízké, můžete k vyřešení použít tzv. Fisherův exaktní test.
Tip na závěr:
Chí-kvadrát test nezávislosti posuzuje vztah mezi kategorickými proměnnými, proto jsou sloupcové grafy skvělým způsobem, jak tato data znázornit. K porovnání podskupin v rámci kategorií použijte například skládaný sloupcový graf.
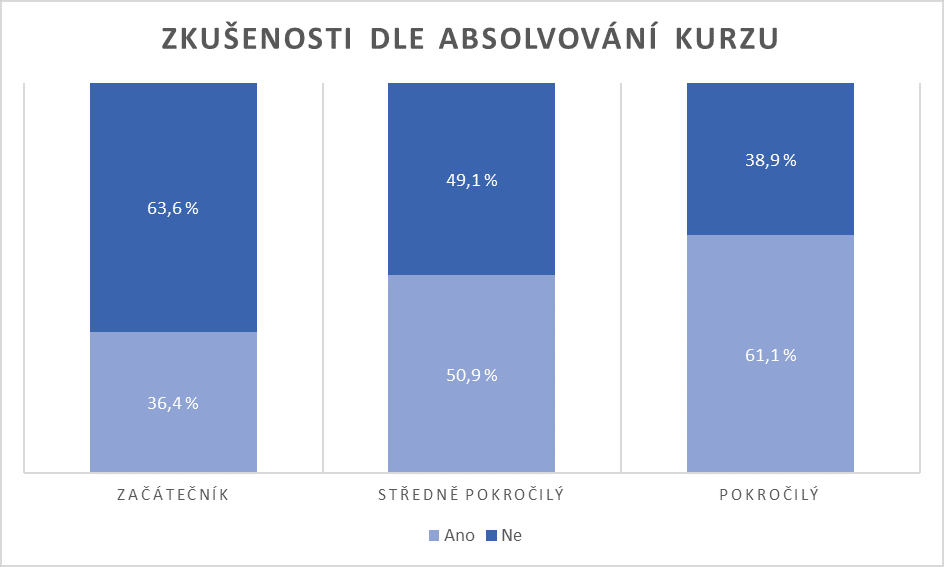
Z grafu lze vidět, že procentuální zastoupení respondentů s absolvovaným kurzem je v každé kategorii dle úrovně zkušeností odlišné. S rostoucí úrovní zkušeností roste i podíl respondentů s absolvovaným kurzem.
Zdroje:
ZVÁRA, Karel. Biostatistika. 2. vyd. Praha: Karolinum, 2003. Učební texty Univerzity Karlovy v Praze. ISBN 80-246-0739-5.